Vibrations
of a rolling tyre
We
investigate vibrations of an unloaded and loaded tyre rolling at constant speed
without slipping in the contact area. A previously proposed analytical model of
a reinforced tyre is considered. The surface of the tyre is represented by
flexible tread, combined with parts of two tori (sidewalls of the tyre). The
contact between the wheel and the ground plane occurs by the part of the tread.
The natural frequencies (NF) and mode shapes (MS) are determined analytically
for unloaded tyre and numerically for loaded tyre. The results were compared
with experiments for the non-rotating tyre. In the case of loaded rotating
tyre, the increasing of the angular velocity of rotation implies that NF
decrease. Moreover, a phenomenon of frequency loci veering is visible here: NF
as functions of angular velocity approach each other and then veer away instead
of crossing. The MS interact in veering region and, as a result, interchange.
|
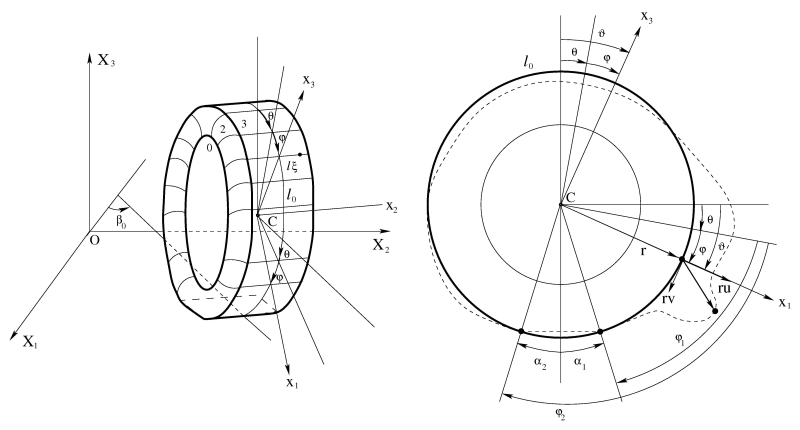
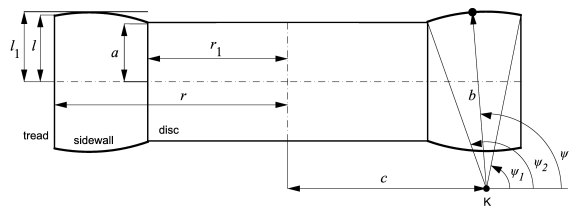
The analytical
model of a wheel with a reinforced tyre |
|
|
|
|
In the
case of loaded non-rotating (LNR) and loaded rotating (LR) tyre, in determining
the frequency of the vibrations, the length of the contact area was taken as
constant, since its variation determines a second order of smallness correction
to the frequency, in the model chosen. For LNR tyre, the increasing of the
contact area (due to the increasing of the vertical load) implies that NF also
increase. In fact, the mass of the vibrating part of the tyre decreases with
the increasing of the contact area, as the tyre does not vibrate in the contact
area. Each mode of an unloaded non-rotating (UNR) tyre is double and for each
NF two identical MS exist. The fixed contact points of the tyre cause a loss of
the circular symmetry. Thus, for each NF of an UNR tyre there are two different
NF of a LNR tyre. This is explained by the disturbance of free wave motion due
to contact. The identical modes split into two not identical ones. The MS
subdivides to a symmetric and an anti-symmetric shapes. For symmetric MS the
corrections to the longitudinal reactions at the boundary points of the contact
area have opposite signs. As for the antisymmetric MS the corrections carry the
same sign. The mass centre of the tyre does not move in the longitudinal
direction for the symmetric MS, and it moves for the antisymmetric MS. Thus,
the antisymmetric MS “sways” from side to side.
|
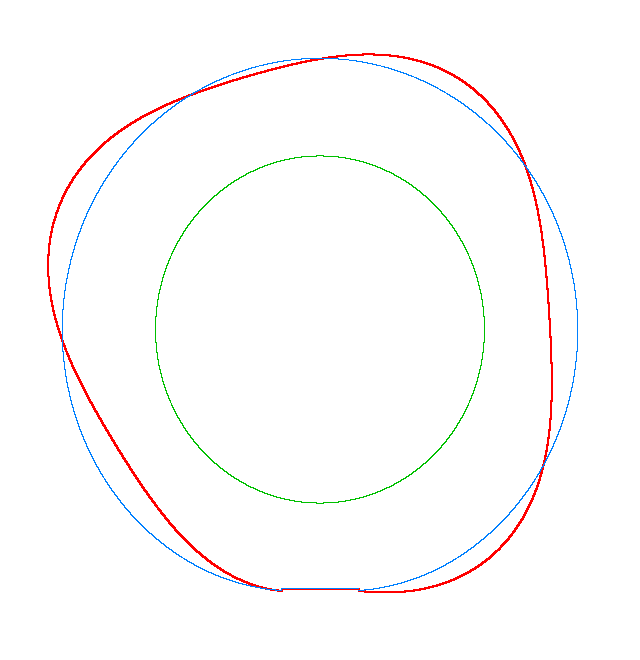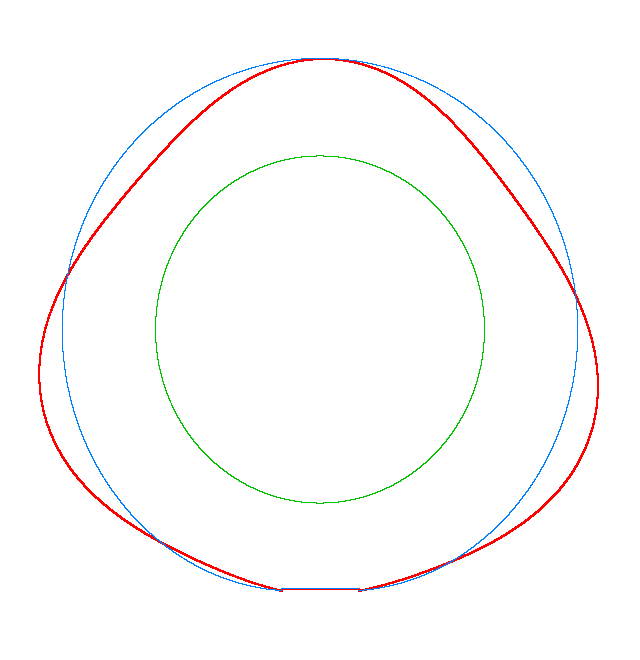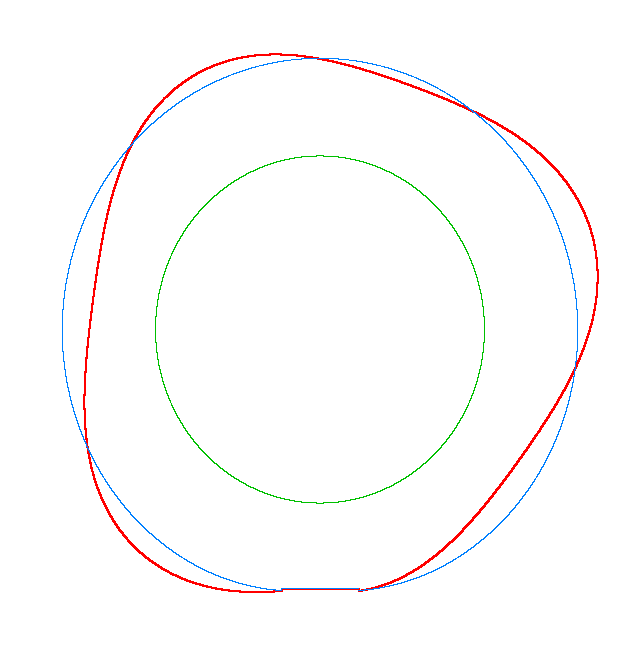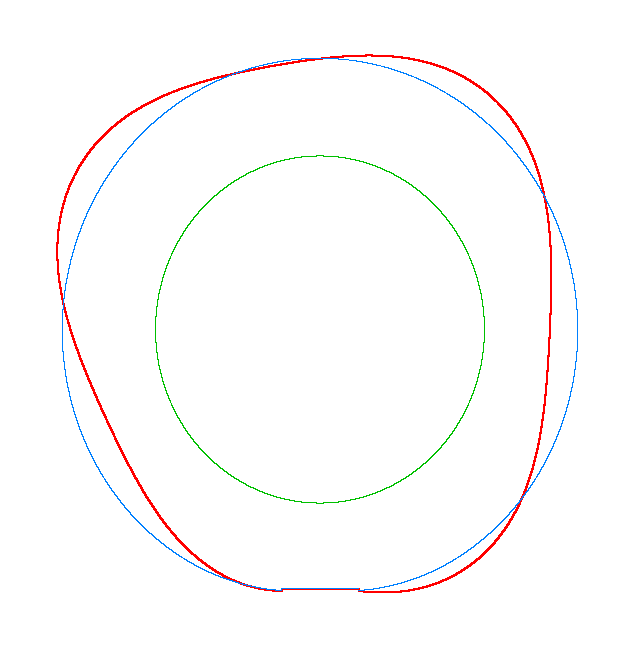
The basic mode
shapes of a loaded non-rotating tyre (Input II, Omega=0 rad/s) |
||
|
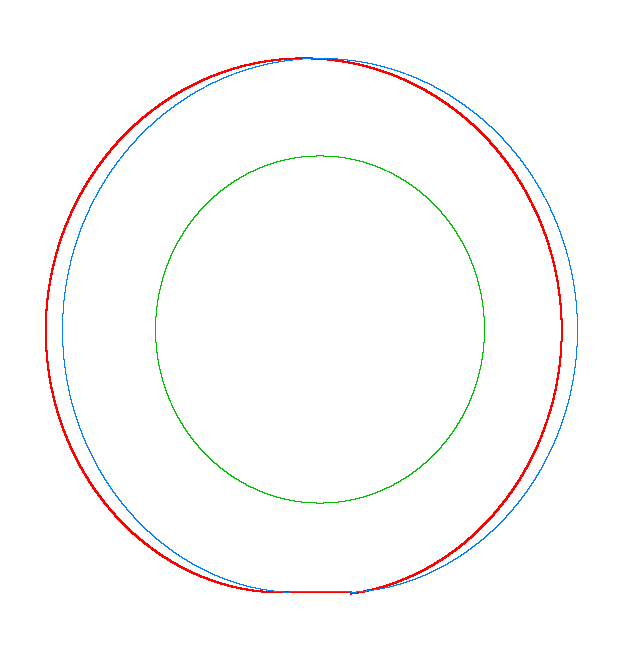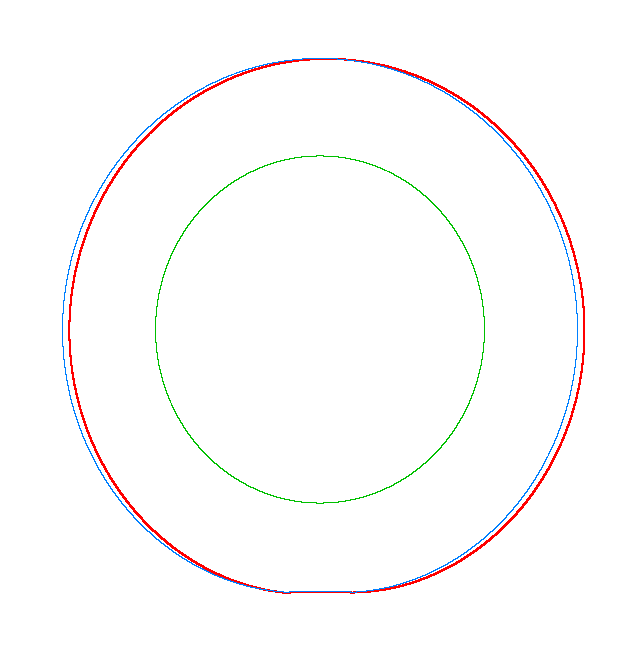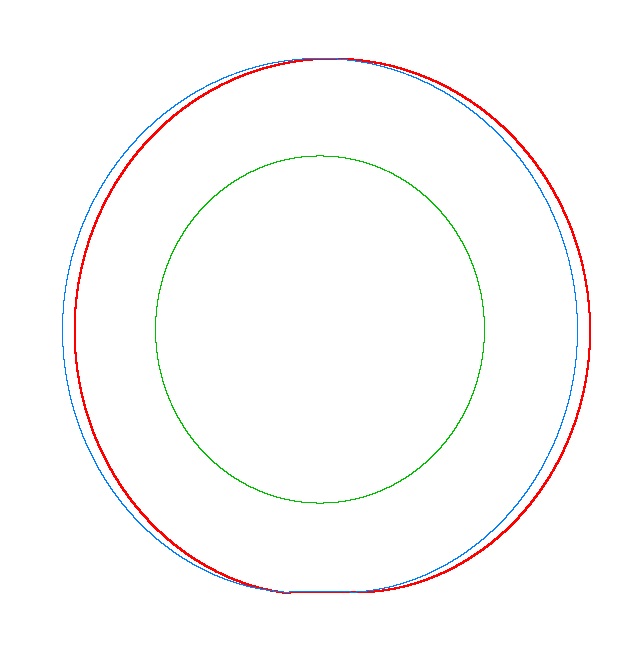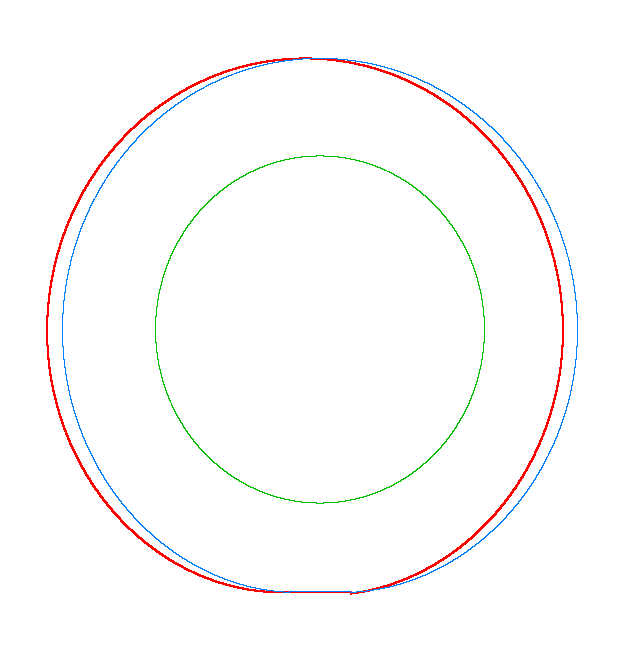
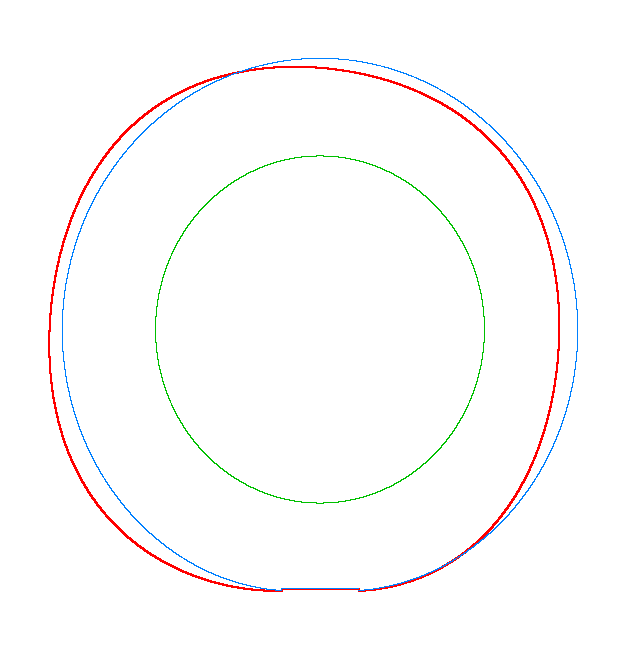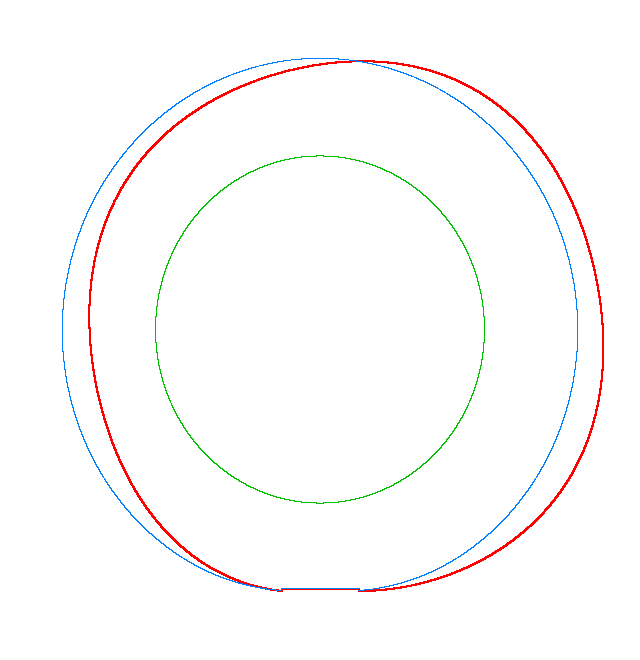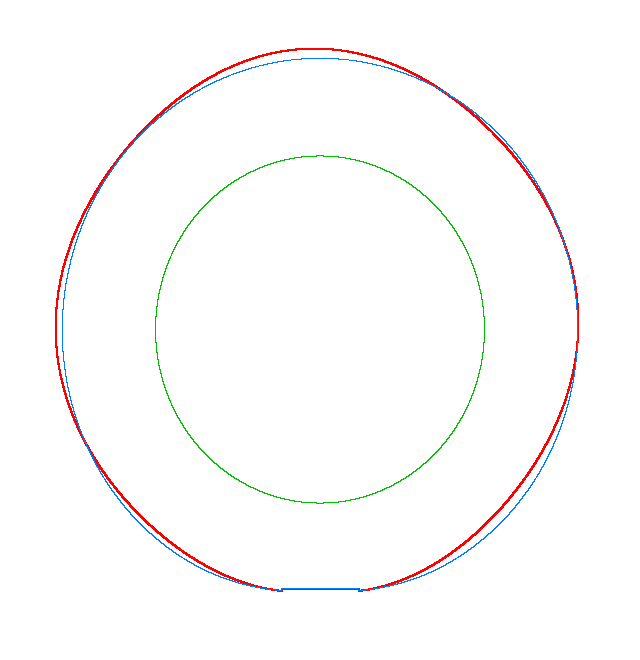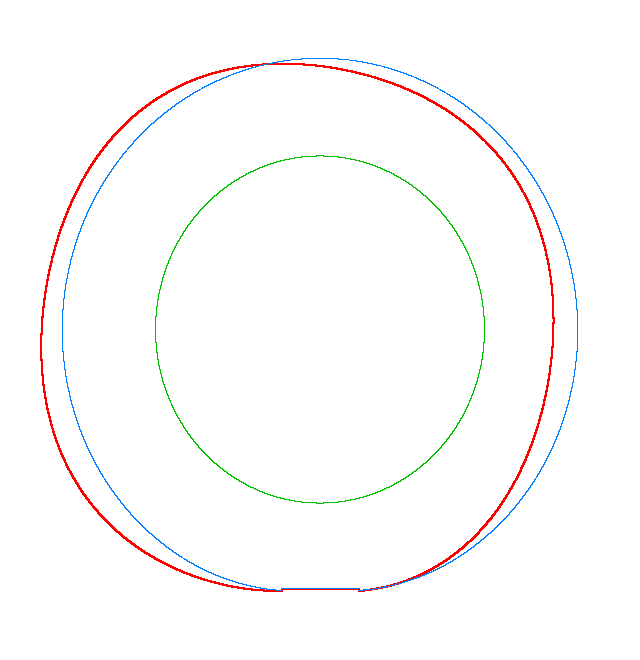
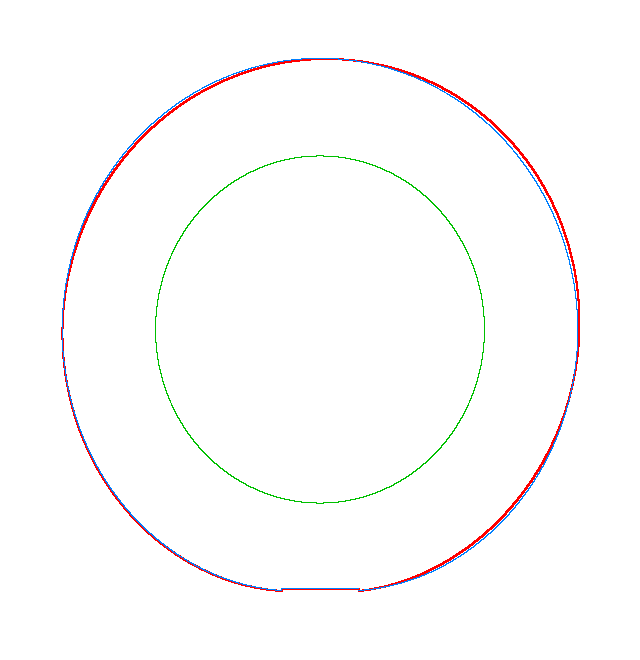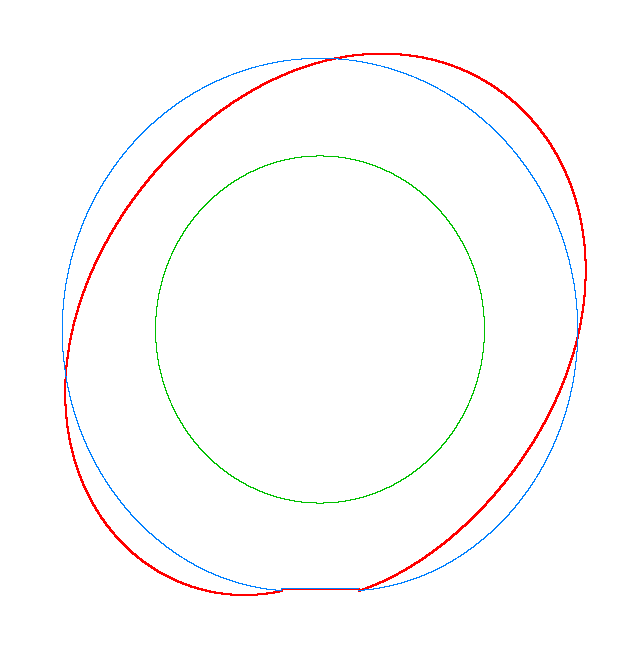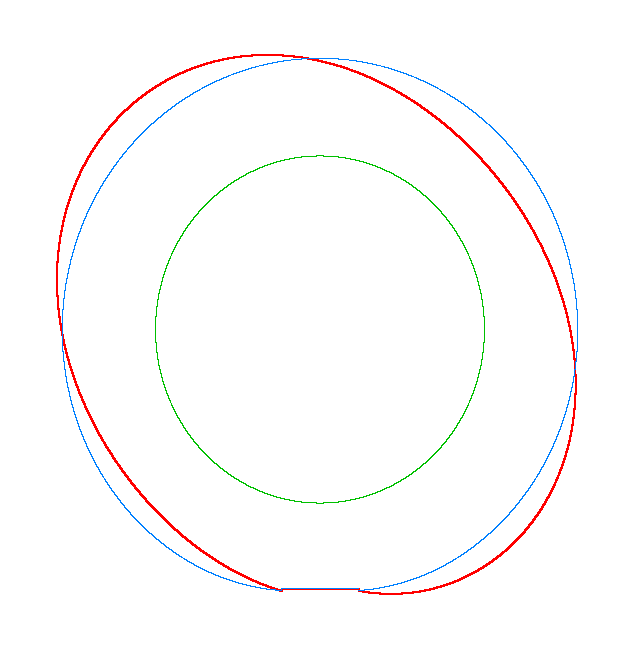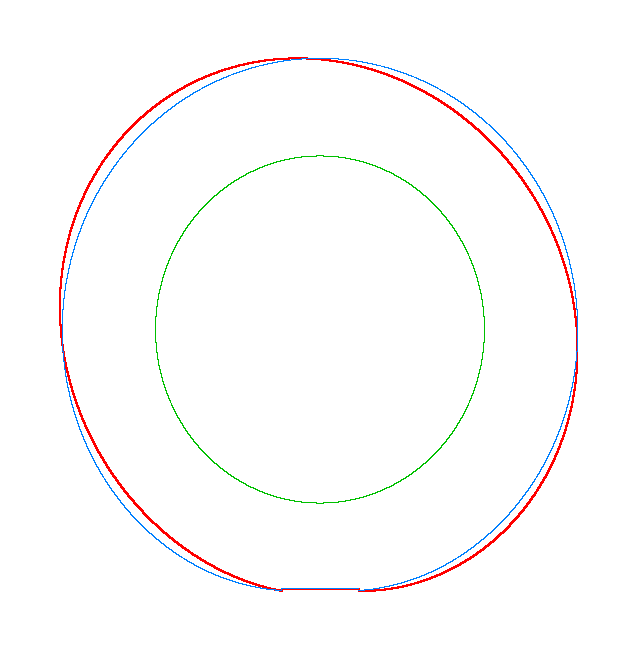
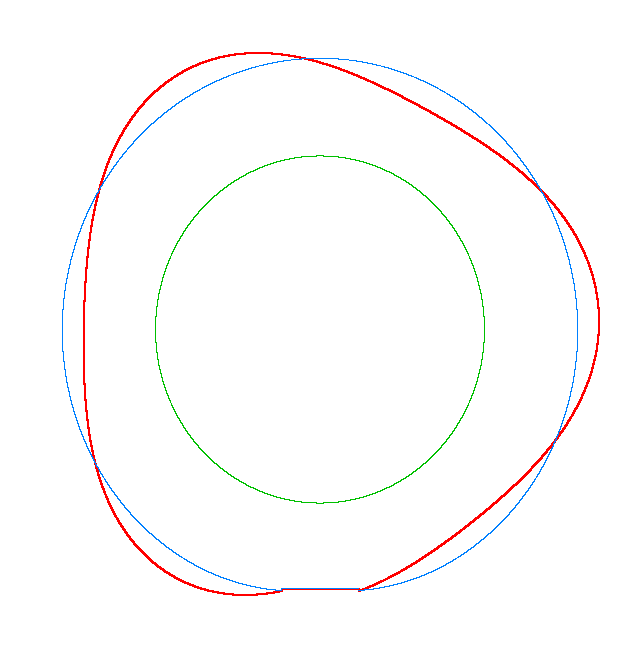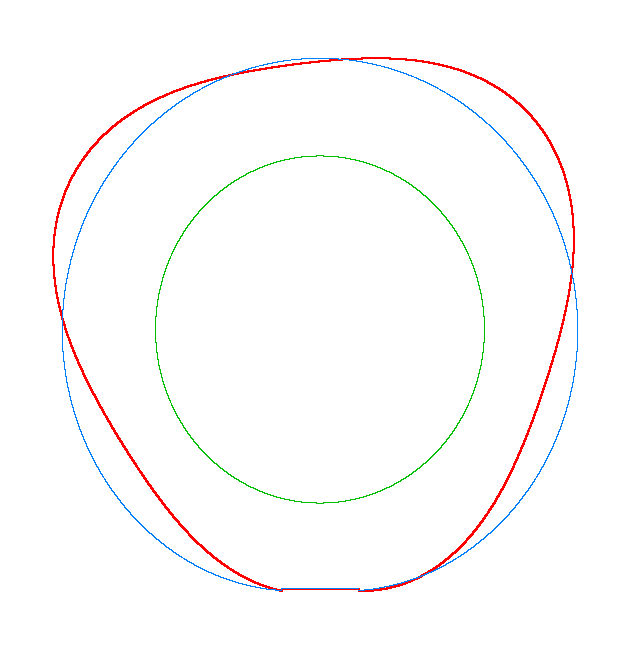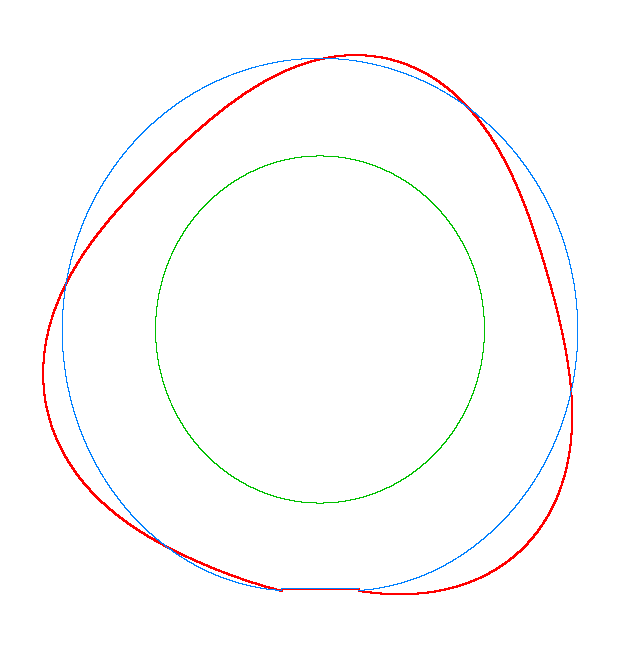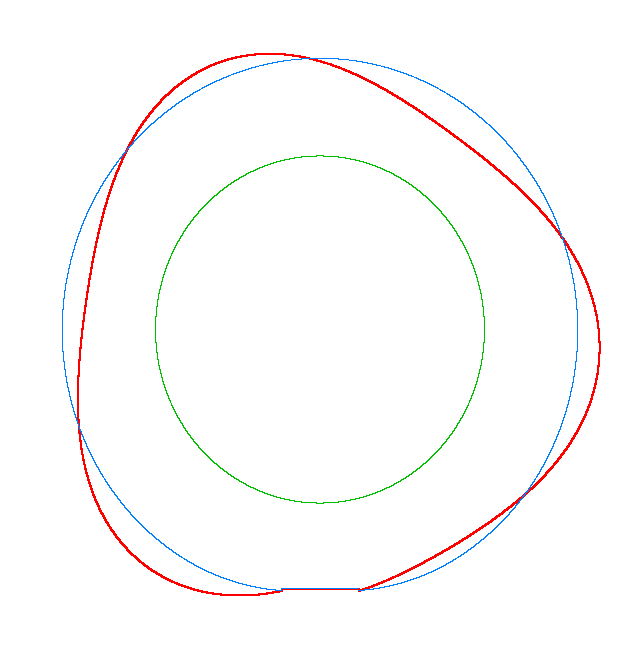
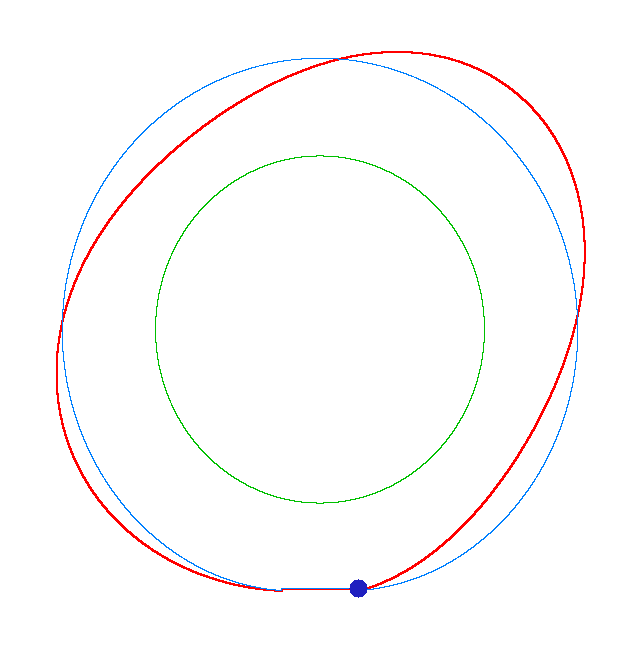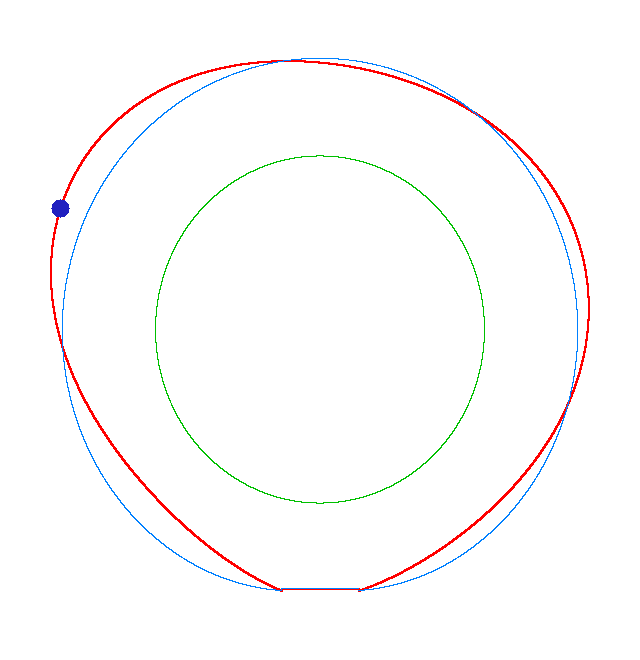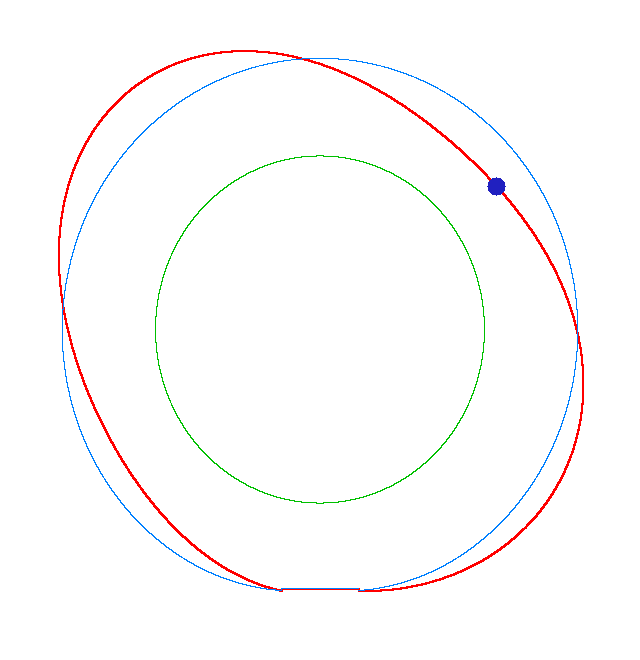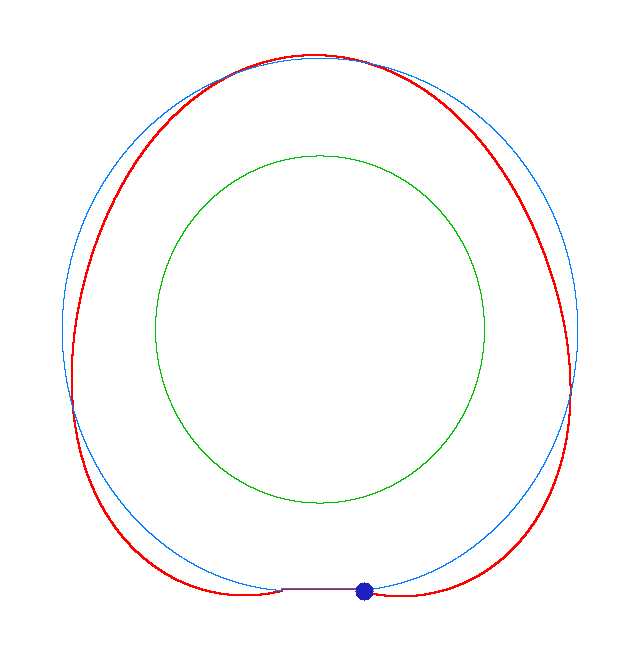
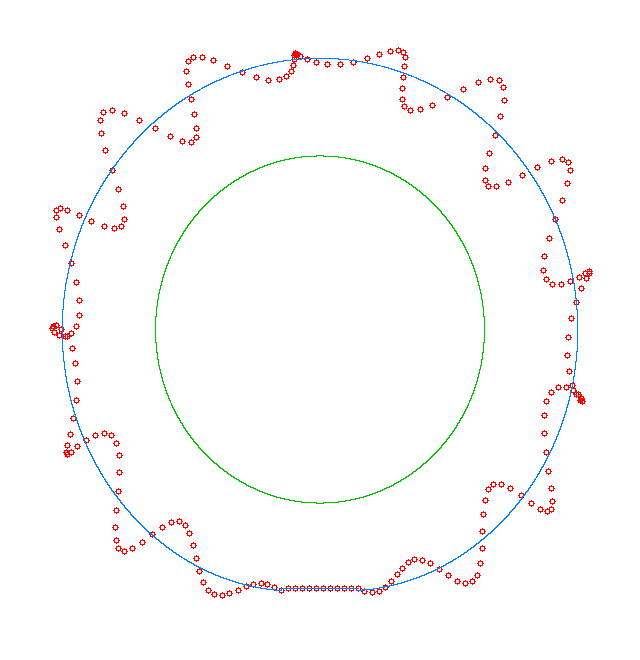
NF1=92.15 Hz |
NF2=99.35 Hz |
NF3=109.72 Hz |
The
quantities of obtained NF for the LNR tyre were compared with the results of
experiment.
|
The test rig for
measurements of NF of an UNR and LNR tyre (2005, LAMI, ENPC) |
|
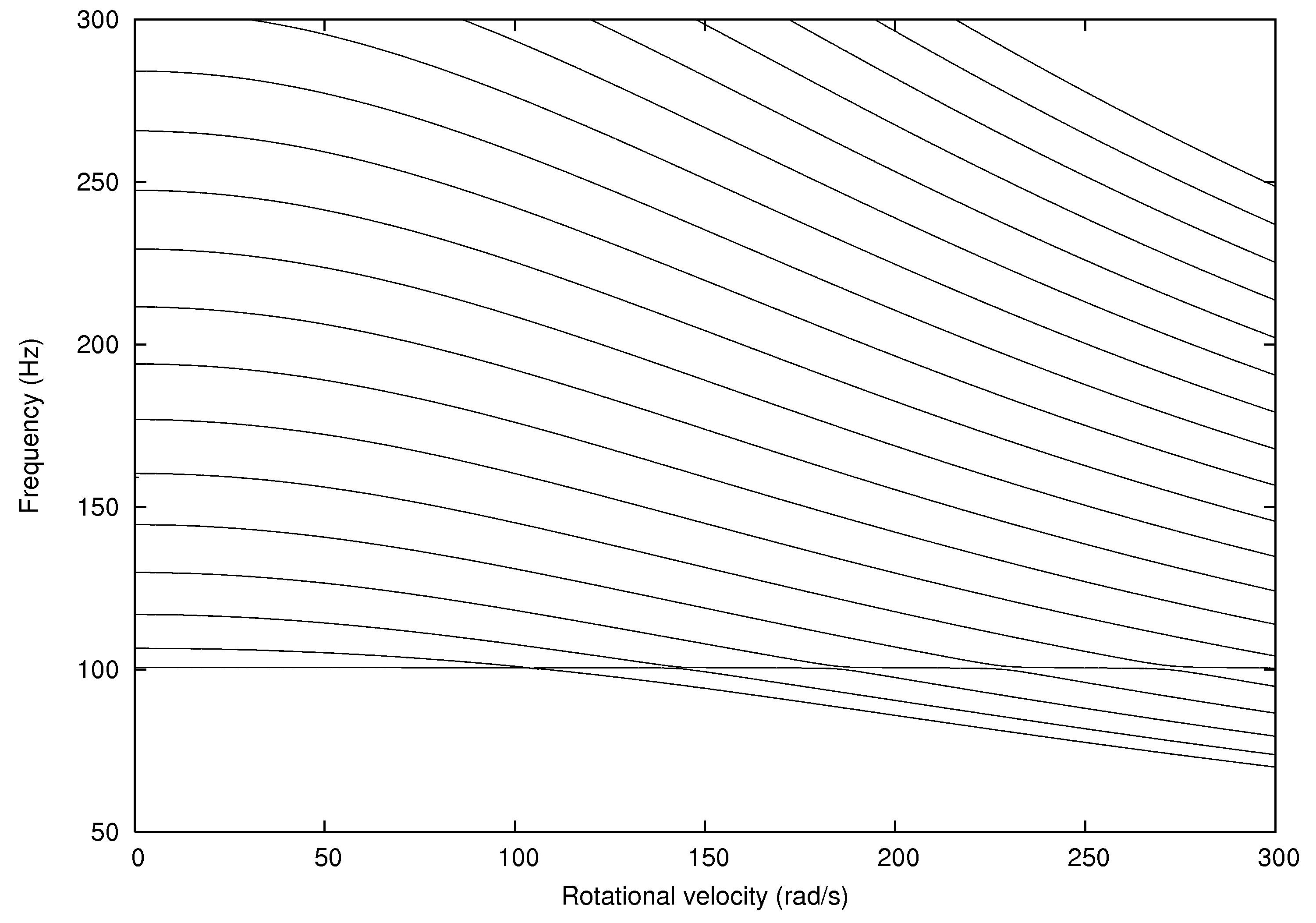
In the
case of LR tyre, the increasing of the angular velocity implies that NF
decrease. The split of NF of an
|
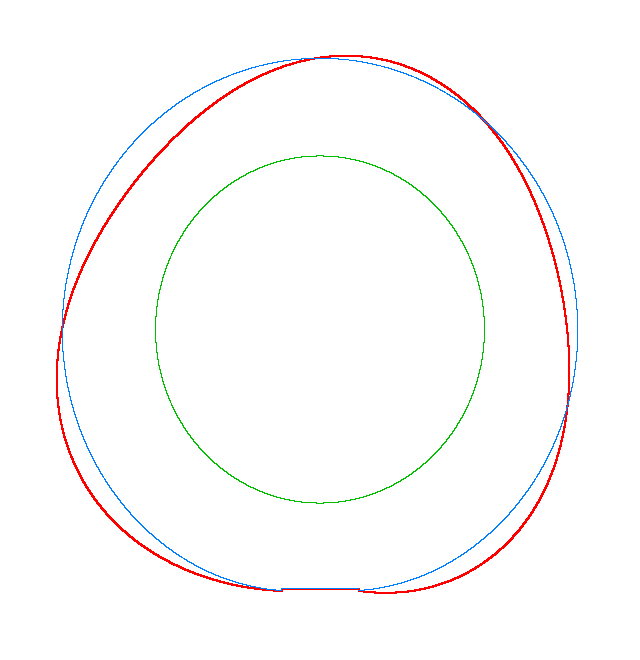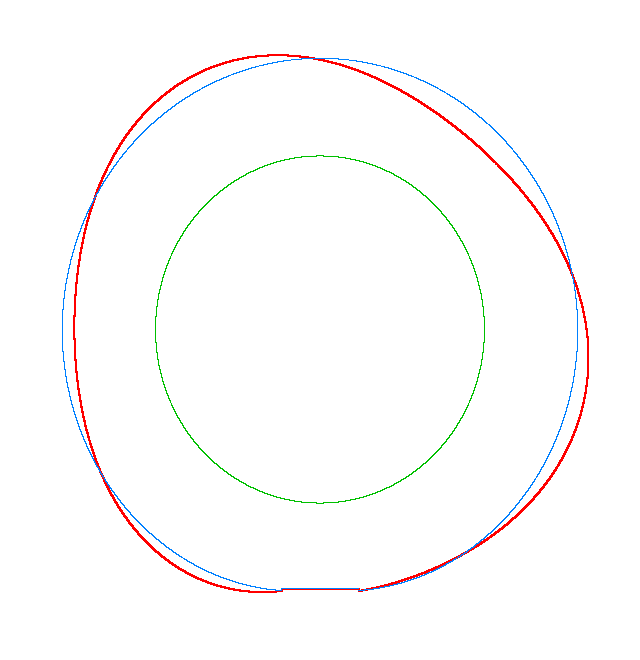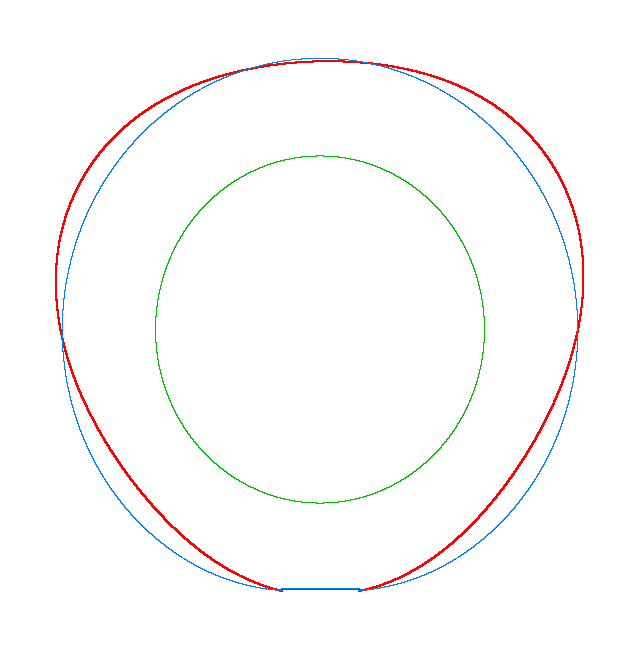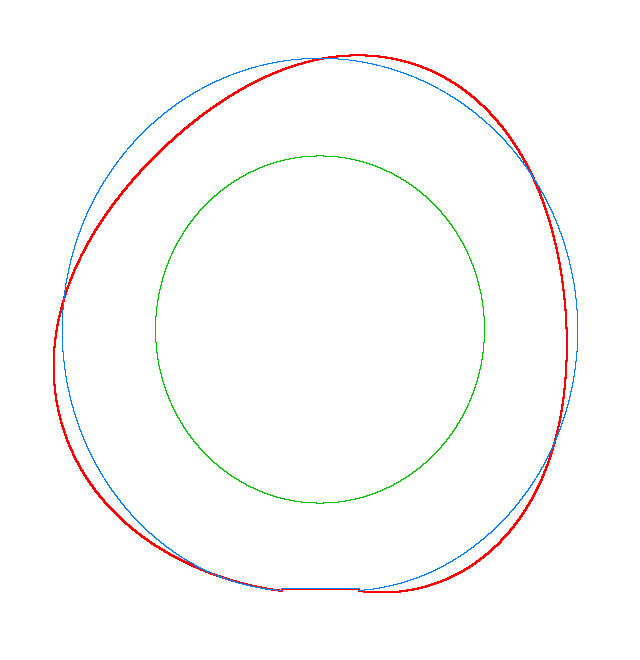
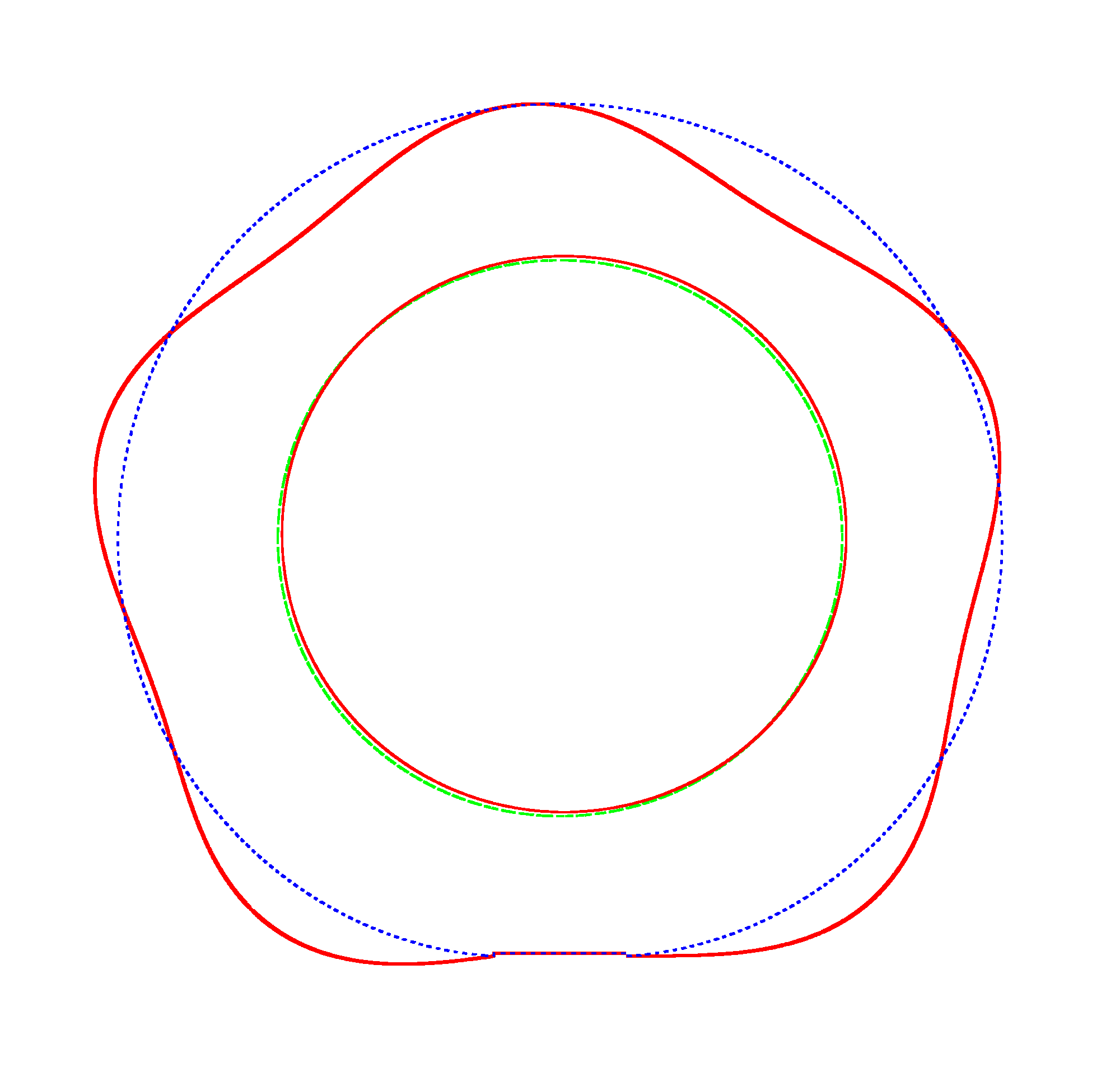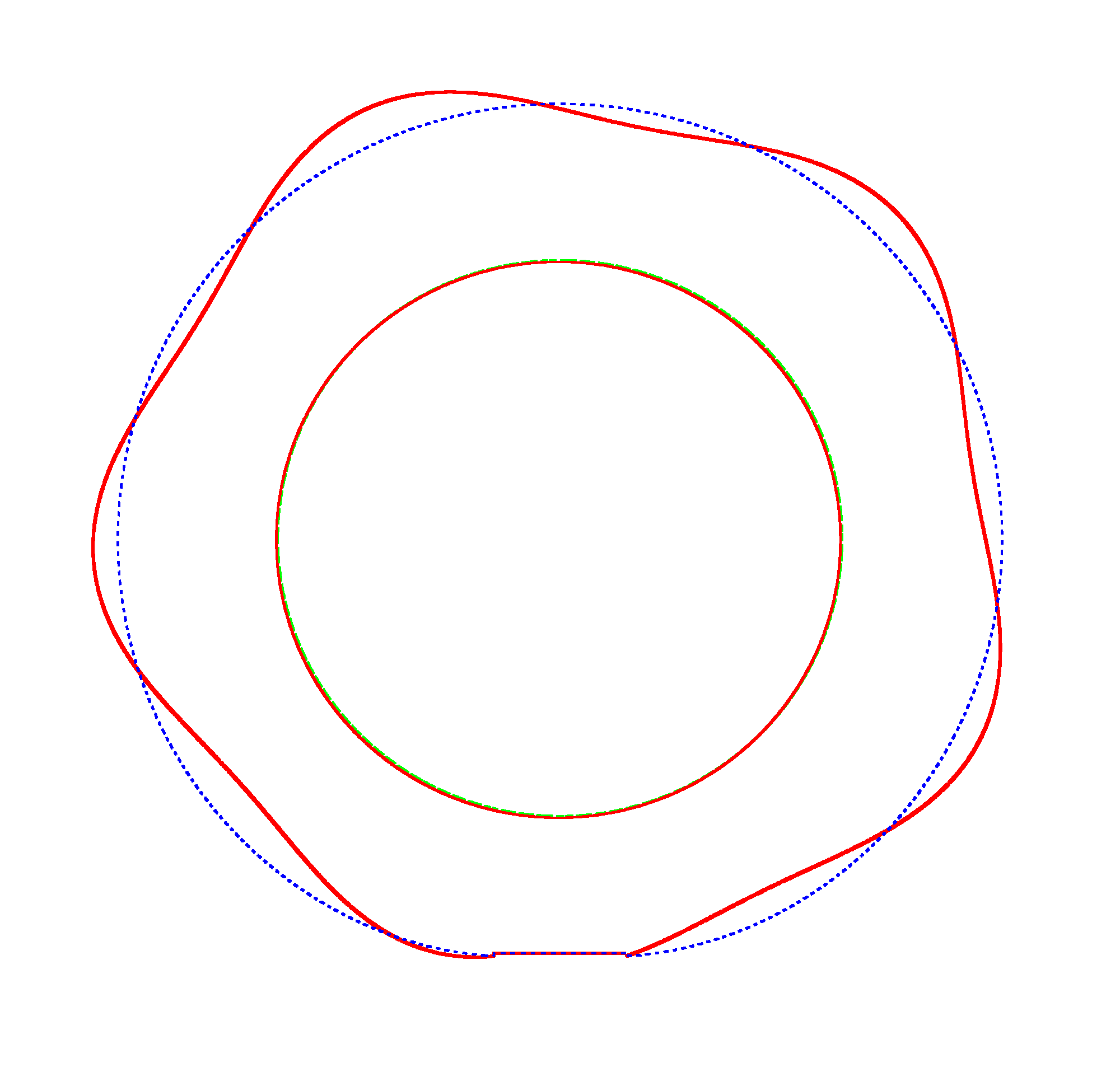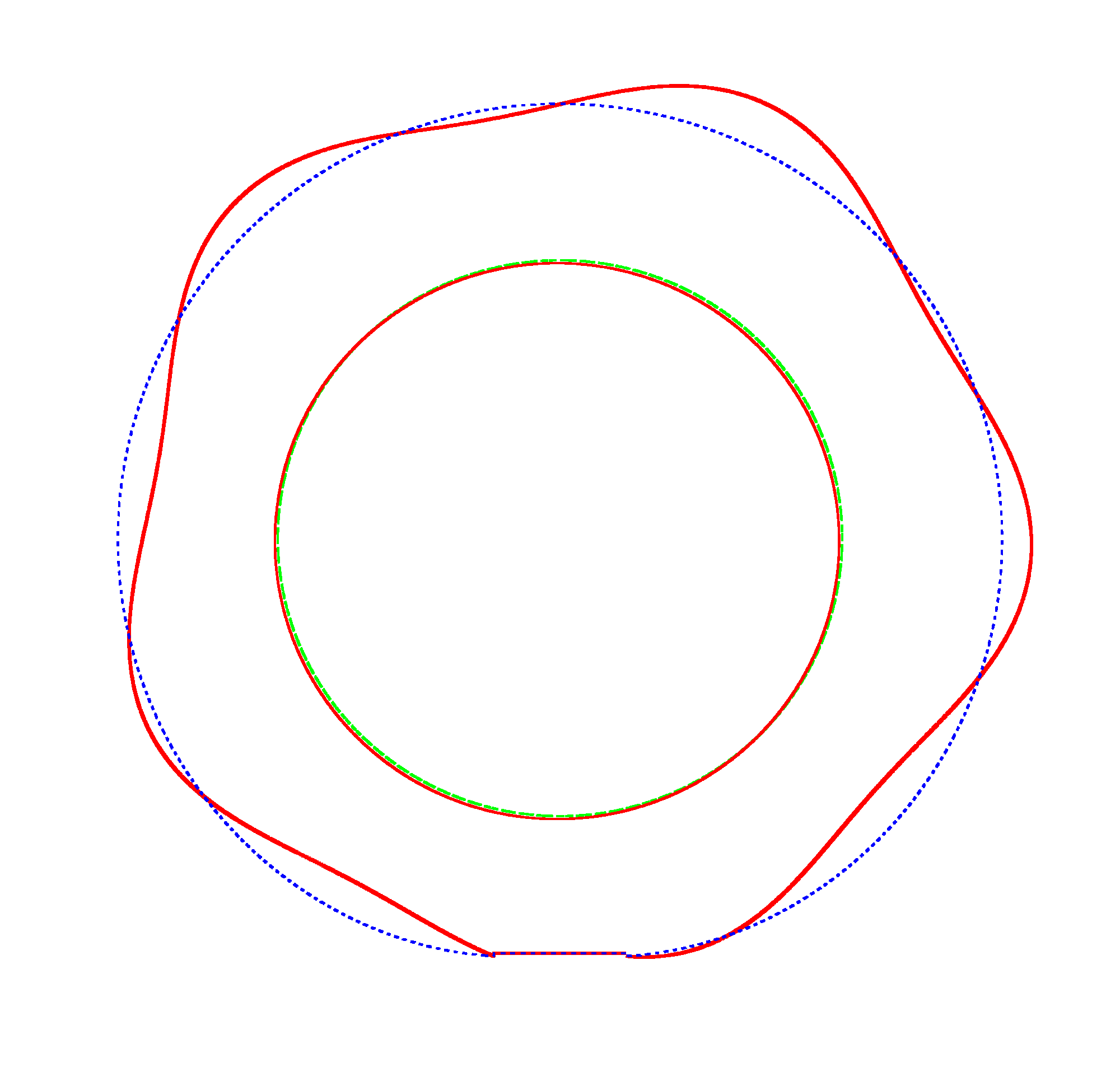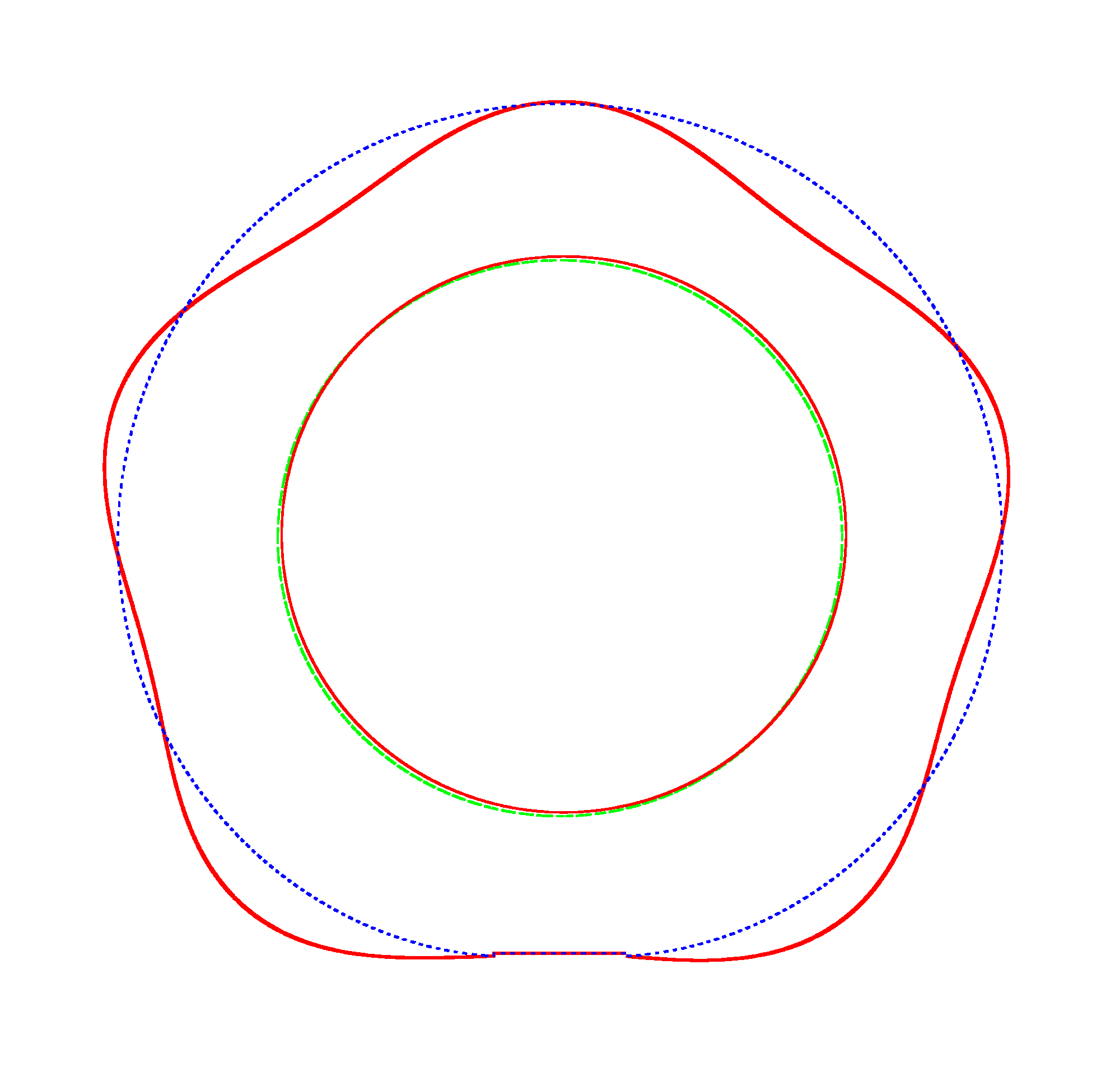
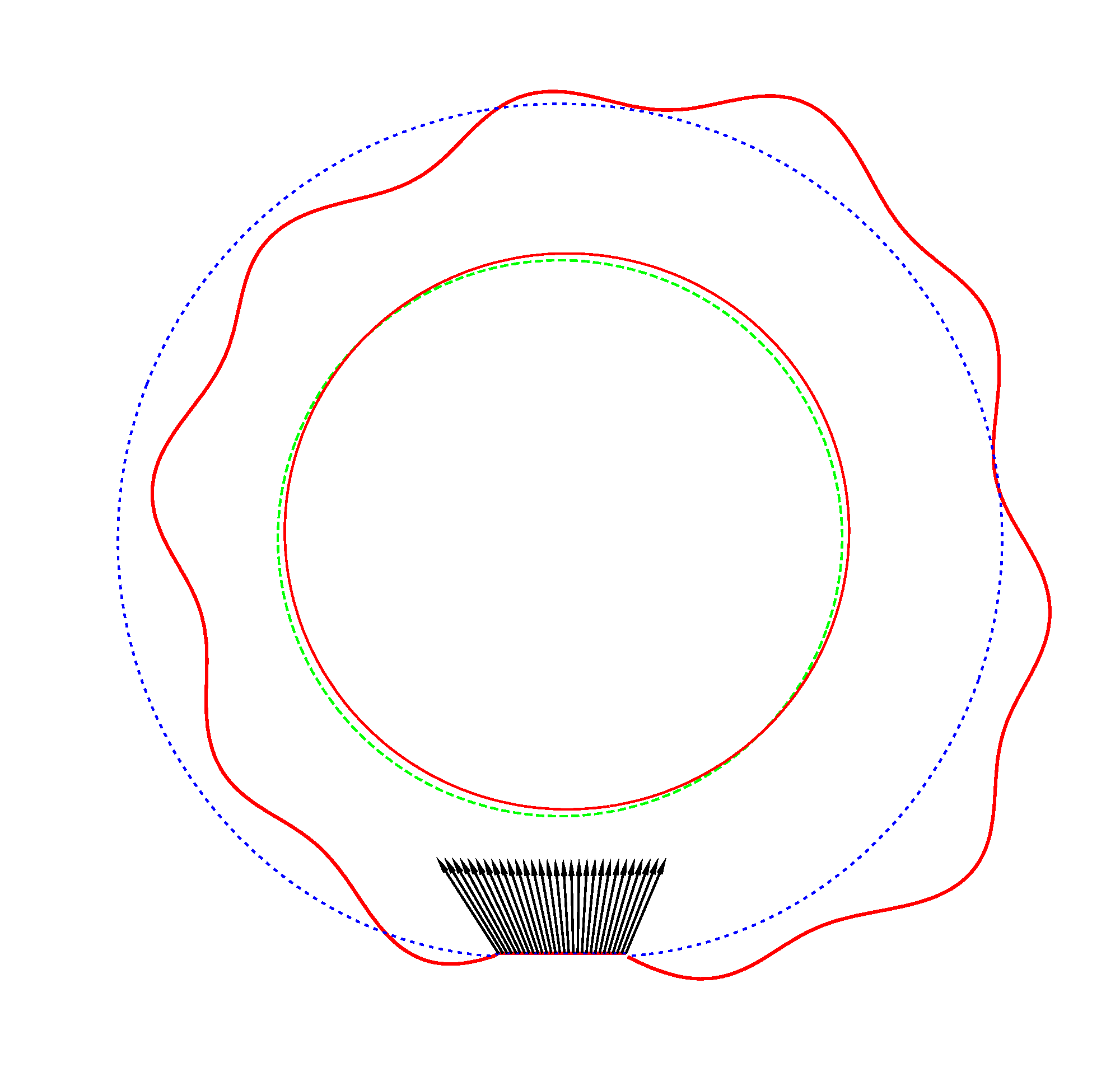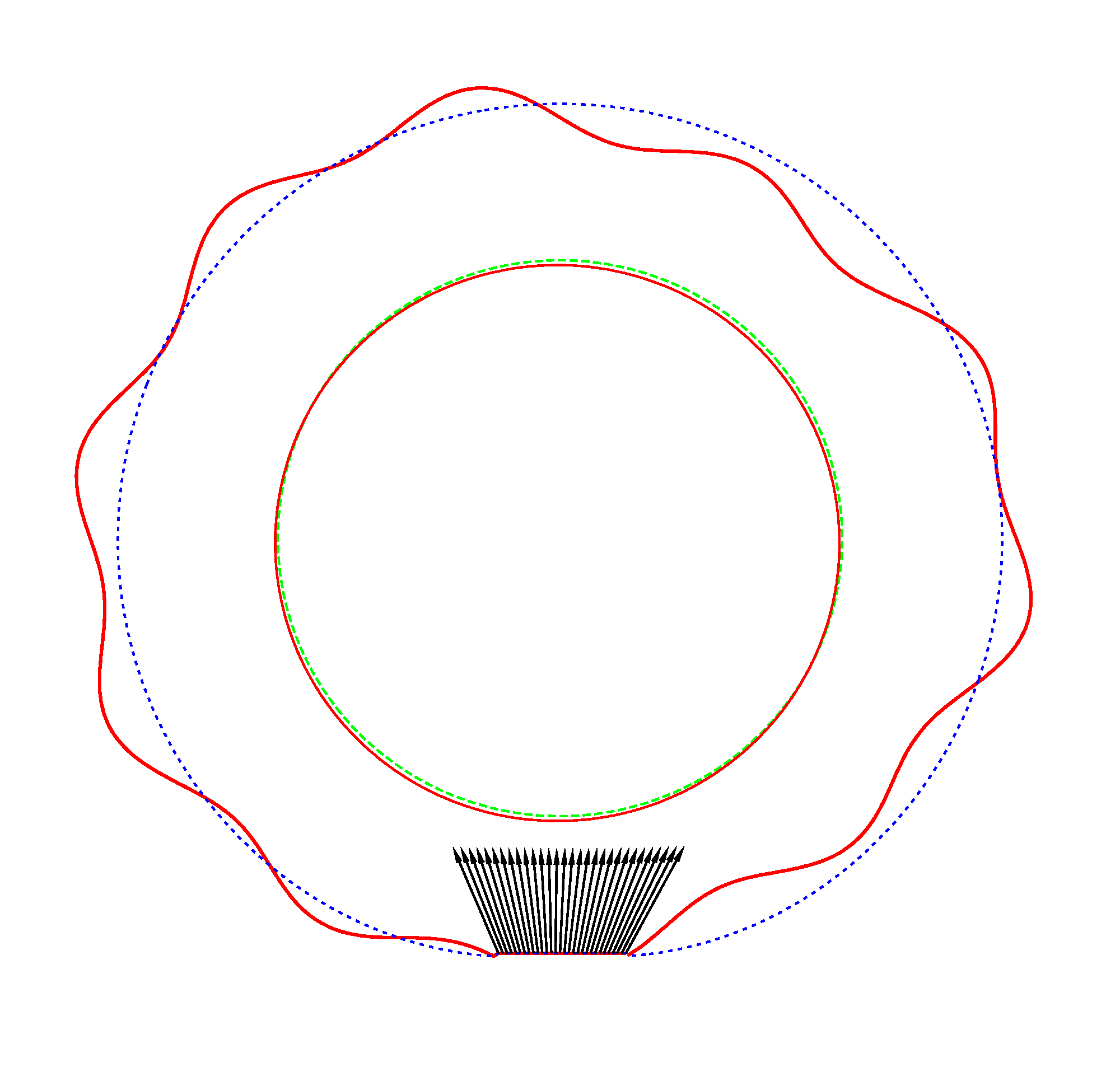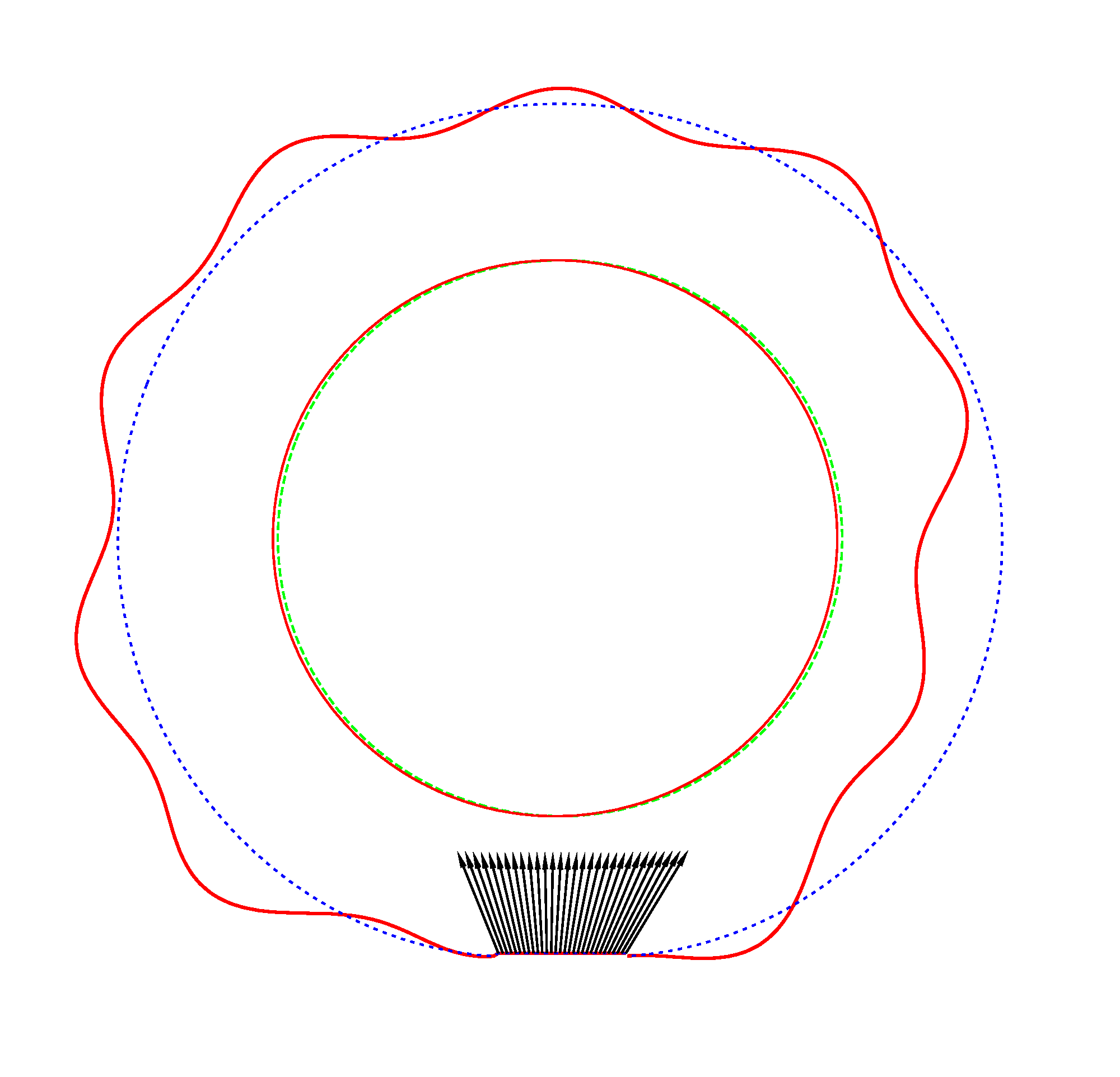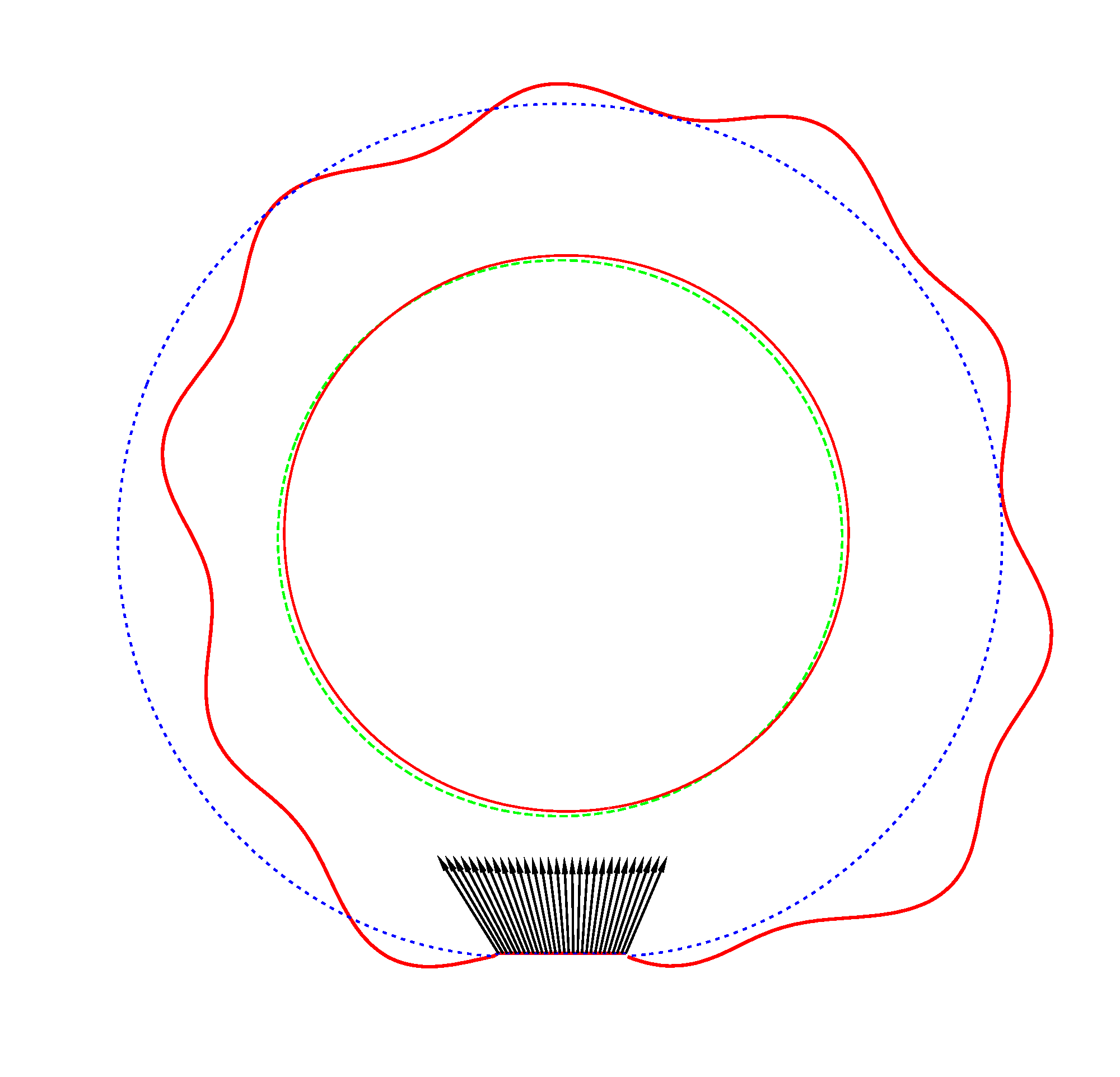
The basic mode
shapes of a loaded rotating tyre (Input I, Omega=175 rad/s), the rolling occurs
in the clockwise direction |
||
|
NF2=94.93 Hz |
NF3=100.46 Hz |
NF5=112.78 Hz |
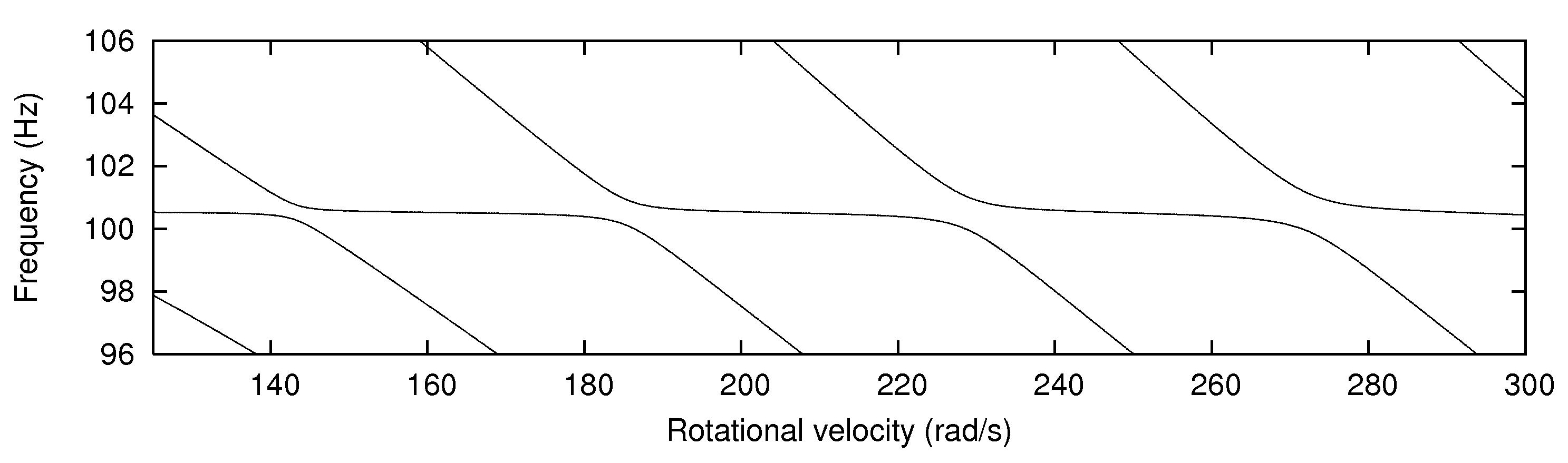
In
addition, an interesting phenomenon of frequency loci veering is visible here:
NF-lines approach each other and suddenly veer away instead of crossing. The MS
interact in frequency loci veering region and finally interchange.
|
The NF as a
function of angular velocity in Eulerian specification (phenomenon of
frequency loci veering) |
|
|
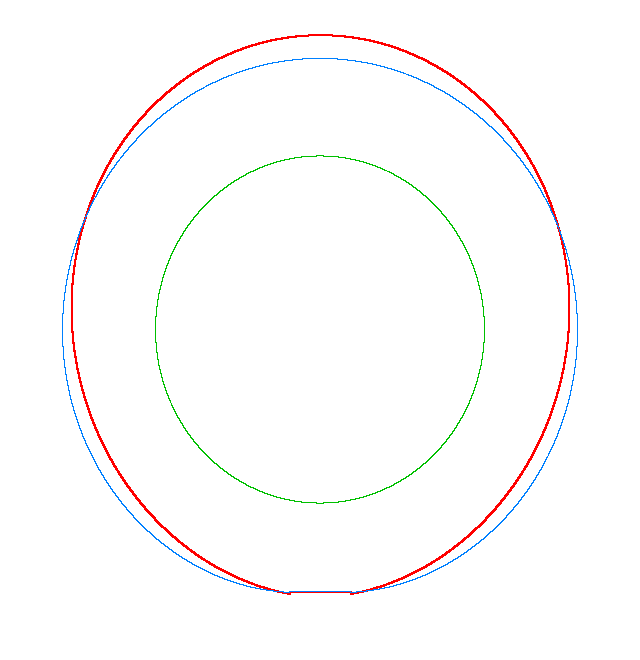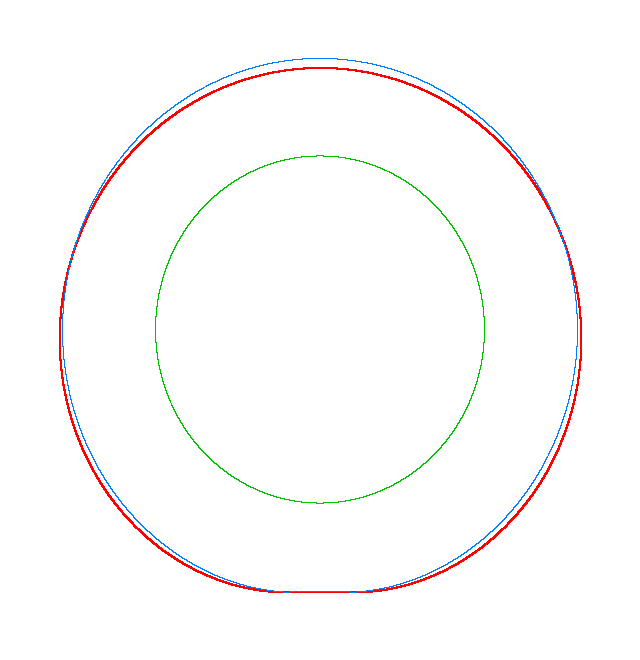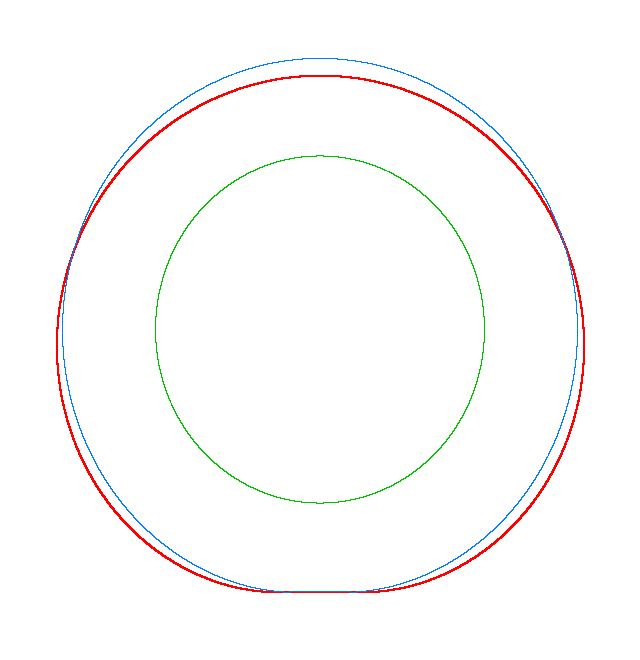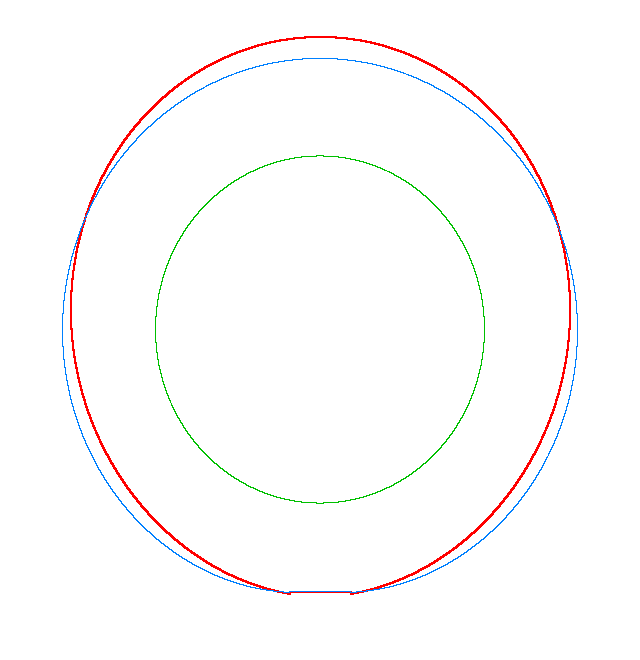
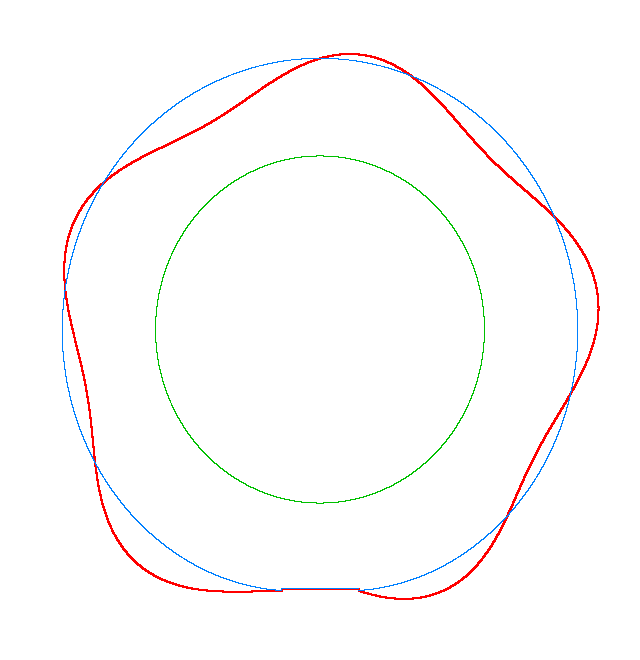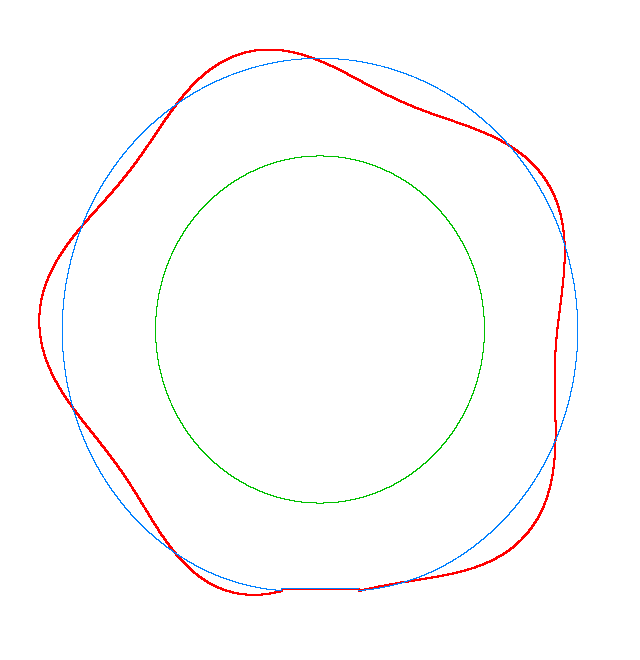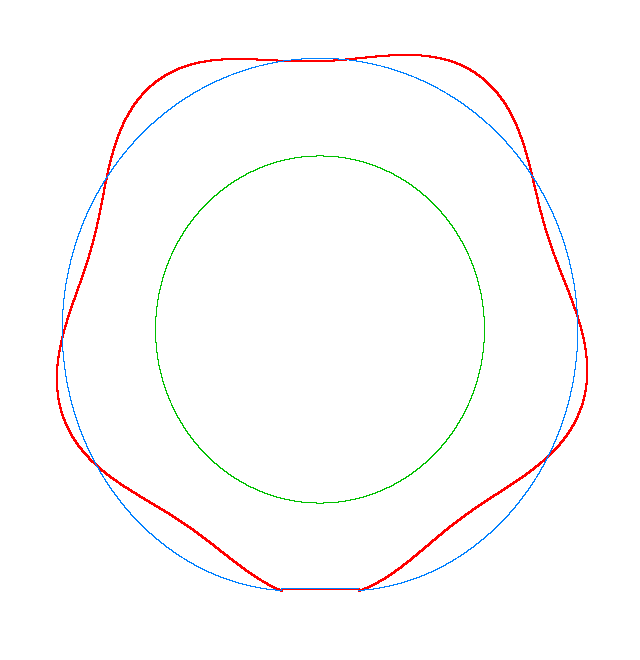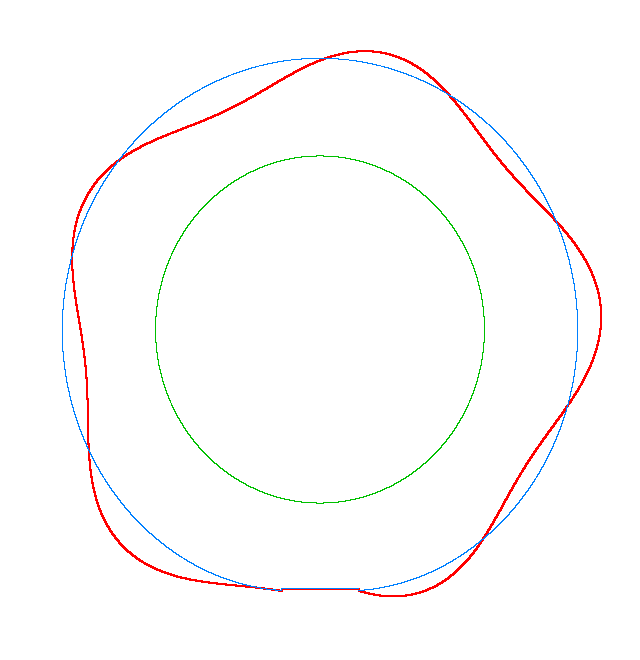
For Omega=3,
100, 130 rad/s the third MS of a LR tyre has, respectively, three, four, five
nodes and is similar to the third, fourth, fifth MS of a LNR tyre. Thus, the
third MS changes from a three-node to a five-node shape, while the NF decreases
from 116.91 Hz to 102.81 Hz.
|
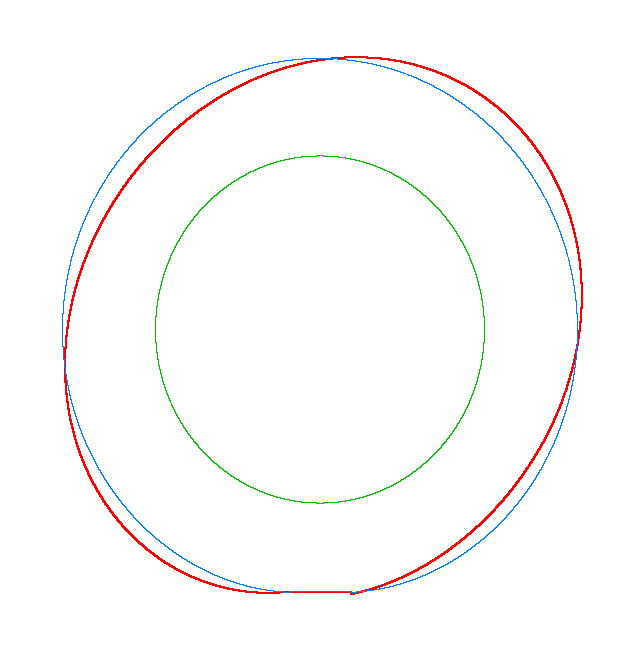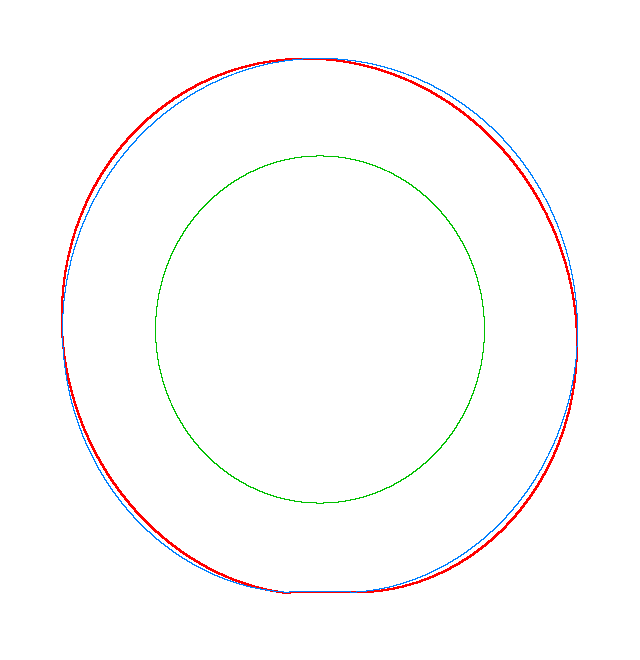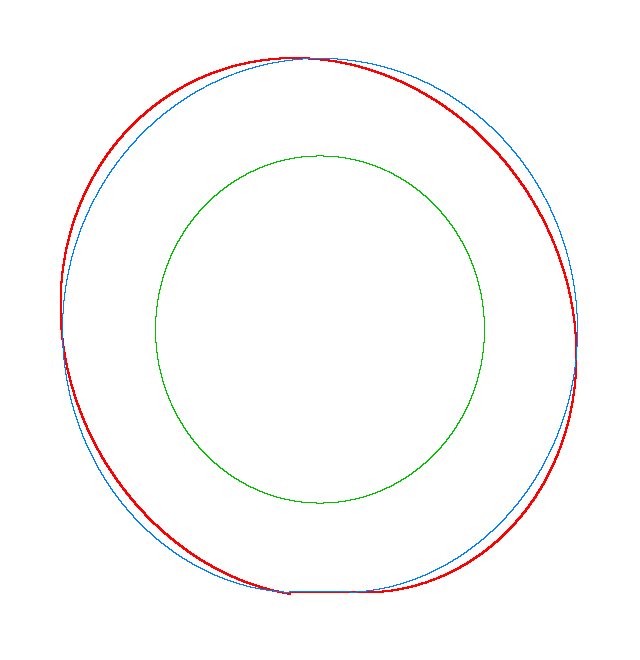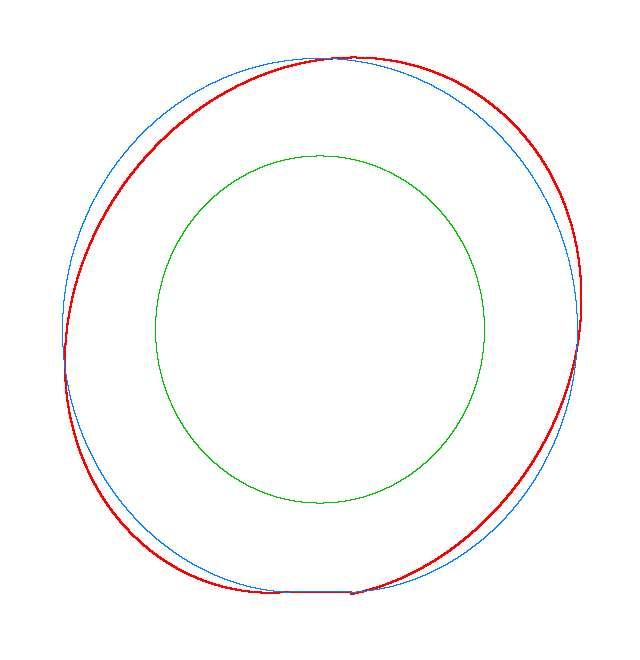
The
evolution of the third mode shape of a loaded rotating tyre (Input I) |
||
|
Omega=3 rad/s, NF3=116.91 Hz |
Omega=100 rad/s, NF3=107.71 Hz |
Omega=130 rad/s, NF3=102.81 Hz |
The movement of a point of tread for the third mode shape of a loaded rotating tyre (Input I, Omega=50 rad/s, NF3=114 Hz) Then we investigate the forced
vibrations of a loaded tyre rolling at constant speed without slipping in the
contact area. In fact, the perturbation (the wheel disc vibrates) of the
previosly considered problem (the wheel disc does not vibrate) is studied. This
perturbation significantly complicates the previously considered case. Now the
external forces and torque applied to the wheel disc, the coordinates of the
mass centre, the components of the reaction in the contact area, the tension of
the tread depend on time. We consider the forced vibrations with harmonic input,
DF_h and DF_v are the driving frequencies in the horizontal and vertical directions. Forced vibrations of a loaded rotating tyre (Input I, Omega=175 rad/s), the rolling occurs
in the clockwise direction
DF_h=115 Hz, DF_v=115 Hz
DF_h=345 Hz, DF_v=345 Hz
DF_h=115 Hz, DF_v=345 Hz
As DF_v=3*DF_h,
then the wheel disc performs two horizontal movements ”left-right” and six
vertical movements ”down-up” per cycle. As the both DF are close to the NF (112.78 Hz and 343.71 Hz), that
is why the two corresponding MS are extracted from the spectrum and are
superimposed on each other (the ”large wave” corresponds to
DF_h and the
”ripple” corresponds to
DF_v). Forced vibrations of a loaded rotating tyre (Input I, Omega=175 rad/s), the rolling occurs
in the clockwise direction
NF=100.46 Hz
DF_h=97 Hz, DF_v=194 Hz
DF_h=97 Hz, DF_v=194 Hz