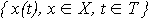- непрерывный сигнал. Введем следующие обозначения: Современные цифровые системы и каналы связи используют выборки сигналов с различными частотами дискретизации. Так, например, в цифровом оборудовании радиостанций и телецентров приняты следующие стандарты на частоту дискретизации: для обработки сигнала 48 кГц; передачи по каналу связи 32 кГц; записи на лазерных компакт-дисках 44,1 кГц. Чтобы обеспечить совместную работу различных источников сигнала, требуется осуществить сопряжение частот дискретизации сигналов, т. е. преобразовать выборку сигнала одной частоты дискретизации в выборку другой частоты. Процесс преобразования выборки сигнала заданной частоты дискретизации к выборке сигнала более высокой частоты дискретизации называется интерполяцией, а обратный процесс преобразования выборки сигнала заданной частоты дискретизации к выборке сигнала более низкой частоты дискретизации - децимацией. Ниже эти преобразования сигнала рассматриваются более подробно.
Рассмотрим задачу интерполяции непрерывного сигнала, заданного произвольной выборкой своих измерений. В этой формулировке задача интерполяции является более содержательной и полезной. Что же касается задачи преобразования выборки сигнала с некоторой частотой дискретизации в выборку сигнала с более высокой частотой дискретизации, то заметим, что непрерывный сигнал можно рассматривать как выборку сигнала с бесконечно большой частотой дискретизации. Поэтому, произвольную выборку сигнала можно получить как простую децимацию непрерывной интерполяции сигнала.
Пусть 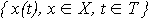- непрерывный сигнал. Введем следующие обозначения:
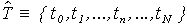- выборка моментов времени измерения сигнала,
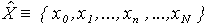- выборка значений координаты сигнала в моменты времени измерения, то есть
.
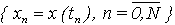Разделим выборку измерений сигнала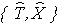 
на группы по М последовательных элементов выборки в каждой группе и представим индекс n, характеризующий элемент выборки измерений сигнала 
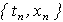, в следующем виде:
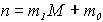 , | (3.1) |
где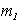 
- номер группы, 
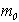- номер позиции соответствующего элемента выборки измерений сигнала в этой группе.
Пусть номер позиции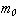 
принимает одно из следующих значений: 
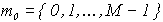, тогда группа, описываемая номером 
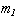, включает выборочные значения сигнала на интервале 
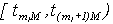, исключая правую граничную точку интервала. Следующая группа, описываемая номером (
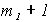) включает выборочные значения сигнала на интервале 
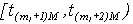и так далее до крайних значений выборки сигнала.
Обозначим через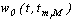 
- некоторую колоколо-образную функцию (окно), выделяющую сегмент сигнала соответствующего группе 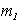на исследуемом интервале времени Т. Например, прямоугольное окно, которое соответствует индикаторной функции сегмента сигнала, можно записать в виде
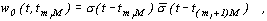
где
,
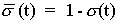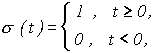
- функция Хэвисайда,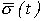 
- дополнительная функция Хэвисайда.
При разделении сигнала на сегменты должно выполняться условие целостности сигнала, т.е.
,
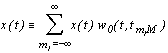из которого следует, что
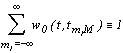 . | (3.2) |
Систему окон, удовлетворяющую условию (3.2), будем называть целостной.
Инфинитную интерполяционную формулу [1] для сигнала x(t) можно записать в виде
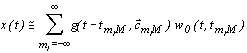 , | (3.3) |
где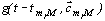 
- сегментная интерполяционная функция.
В качестве сегментной интерполяционной функции обычно используют линейную функцию по параметрам
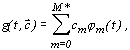 | (3.4) |
где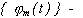 
заданное семейство базисных функций. Параметры 
=
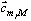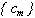определяют из условия равенства сегментной интерполяционной функции выборочным значениям сигнала в узлах интерполяции, т.е.
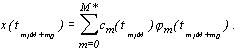 | (3.5) |
В формуле (3.5) число параметров M* сегментной интерполяционной функции может отличаться от числа измерений М, лежащих на выбранном сегменте сигнала. Если M*>M, то для определения значений параметров сегментной интерполяционной функции можно использовать измерения сигнала, принадлежащие соседним сегментам интерполяции. В этом случае инфинитная интерполяционная функция (3.3) будет непрерывной функцией не только внутри, но и на границах сегментов сигнала.
Пусть M* = М + v , где v > 0 . Матрица системы уравнений (3.5) имеет вид
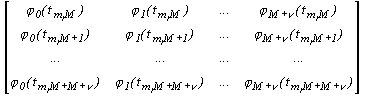 | (3.6) |
Для однозначного вычисления значений параметров 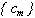сегментной интерполяционной функции необходимо, чтобы определитель матрицы (3.6) был отличен от нуля. В этом случае значения параметров 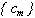можно найти по формуле
,
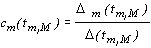где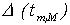 
- определитель матрицы (3.6), 
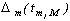- определитель 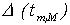, в котором элементы m-го столбца заменены столбцом 
.
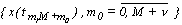Cегментную интерполяционную функцию теперь можно переписать в виде
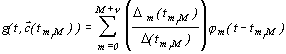 . | (3.7) |
Если определитель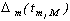 
разложить по элементам m-го столбца
,
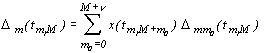где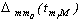 
- соответствующее алгебраическое дополнение, и подставить в (3.7), получим выражение для инфинитной интерполяционной функции (3.3) непосредственно через заданные значения измерений координаты сигнала, т.е.
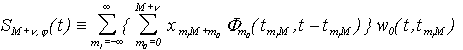 | (3.8) |
где функция
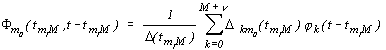
удовлетворяет условию
,
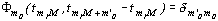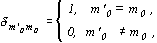
- символ Кронеккера.
В качестве сегментной интерполяционной функции часто используют степенные многочлены
,
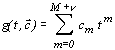для которых инфинитная интерполяционная формула (3.8) имеет вид
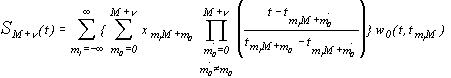 | (3.9) |
Формула (3.9) представляет инфинитную интерполяционную формулу Лагранжа, которая строится по М выборочным значениям сигнала, принадлежащим текущему сегменту, и v+1 выборочному значению сигнала, принадлежащему соседнему или соседним сегментам.
Интерполяционная формула (3.9) асимптотически соответствует формуле Котельникова для равномерной выборки сигнала. Действительно, интерполяционную формулу Лагранжа для инфинитного сегмента сигнала можно записать в виде
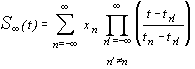 . | (3.10) |
В случае равномерной выборки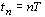 
, где T - интервал между измерениями или шаг дискретизации сигнала. Введем переменную 
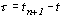и подставим в (3.10). Выражение под знаком произведения можно привести к виду
.
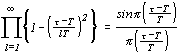Учитывая, что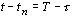 
, интерполяционную формулу Лагранжа для инфинитного сегмента сигнала в случае равномерной выборки измерений с шагом Т можно представить в виде
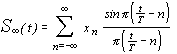 . | (3.11) |
Выражение (3.11) совпадает с формулой Котельникова (1.1).
Рассмотрим некоторые важные частные случаи инфинитной интерполяционной формулы (3.9). Наиболее простое выражение инфинитная интерполяционная формула имеет для кусочно-постоянной интерполяции между измерениями сигнала
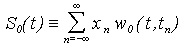 . | (3.12) |
Кусочно-линейной интерполяции между измерениями сигнала соответствует выражение
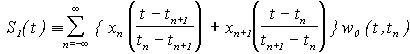 . | (3.13) |
Это выражение можно переписать в виде инфинитной интерполяционной функции с триангулярным окном [2]
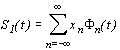 , | (3.14) |
,
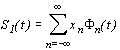где
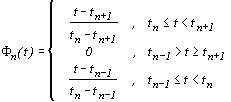 | (3.15) |
- триангулярное окно.
Преобразование выборки сигнала заданной частоты дискретизации к более высокой частоте описывается формулами (3.8-9), в которых вместо непрерывного времени (t) следует подставить соответствующую выборку моментов времени измерений сигнала. Заметим, что на практике обычно используются кусочно-постоянная или кусочно-линейная интерполяции выборочных значений сигнала (3.12-13), ввиду их простой реализации.
В отличие от процедуры интерполяции преобразование выборочных значений сигнала к более низкой частоте дискретизации может являться источником специфической ошибки, которую часто называют подменой частот [3]. Как упоминалось выше (см. ╖1), эффект подмены частот проявляется при выборе слишком низкой частоты дискретизации сигнала, т. е. ниже удвоенной максимальной частоты фурье-спектра сигнала. В этом случае нарушаются условия теоремы Котельникова и высокочастотные гармоники сигнала или гармоники, частота которых выше половины выбранной частоты дискретизации, воспринимаются в полученной выборке как низкочастотные гармоники, т. е. гармоники, частота которых ниже половины частоты дискретизации.
Чтобы избежать этого стробоскопического эффекта требуется подавить высокочастотные гармоники сигнала, частота которых выше половины выбранной частоты дискретизации сигнала. Для этого используются линейные цифровые фильтры низких частот.
Децимацию с нецелым коэффициентом сжатия частоты дискретизации аппроксимируют дробью, числитель которой определяет интерполяцию сигнала в целое число раз, а знаменатель - децимацию сигнала также в целое число раз. Интерполяция сигнала была рассмотрена выше, поэтому достаточно рассмотреть децимацию сигнала с целочисленным коэфициентом сжатия частоты дискретизации.
Реализация децимации сигнала с целым коэффициентом (p:1) очевидна: выходная выборка должна содержать лишь каждый p-тый элемент исходной выборки, подвергнутой соответствующей цифровой фильтрации. При этом какого-либо определенного правила выбора типа фильтра несуществует, так как помимо индекса децимации выбор типа фильтра диктуется многими факторами, в частности, используемым программным и аппаратным обеспечением. Более широко используются нерекурсивные цифровые фильтры или фильтры с конечной импульсной характеристикой (КИХ-фильтры), так как в этом случае требуется вычислять только каждый p-тый элемент исходной выборки. В этом состоит некоторое преимущество использования нерекурсивных цифровых фильтров при выполнении процедуры децимации цифровых сигналов.
1. Чичагов А.В. Математическое моделирование сигналов. М.: ВЦ РАН, 1995.
2. Гольденберг Л. М., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов. М.: Радио и связь, 1990.
3. Рабинер Л.Р., Гоулд В. Теория и применение цифровой обработки сигналов. М.: Мир, 1978.